Molecular dynamics (MD) is a ubiquitous tool used to capture the dynamic evolution of molecular systems, where a finite difference approximation is used to integrate Newton’s equations of motion with a time step on the order of femtoseconds. One of the most significant challenges for long-timescale MD simulations is the prohibitively high computational cost, especially when energies and forces are ab initio computed. Developing a computationally efficient potential energy surface (PES) with an accurate description of the atomic interactions provides a solution to overcome the limitation of MD in system size and timescale. Recently, machine learning techniques, especially artificial neural networks (ANN), have been shown to predict properties of materials with reasonable accuracy and efficiency.

Most of the machine learning techniques interpolate the first principles potential energy surface (FP-PES) by a set of reference calculations of different local minimums prior to the simulation of interest. Unfortunately, application of these methods for MD is circumscribed by the following two factors: (1) traditional ANN potentials were commonly trained by a finite number of reference calculations on local minimums, which could lead to a considerable error at regions that are not well represented by training dataset. (2) To the best of my knowledge, none of these ANN potentials were trained against atomic forces. The error in ANN energy can be significantly amplified and propagated to the ANN atomic forces when the derivative is taken. The above two limitations affect the validity of the MD with current ANN potentials, which calls for an innovated ANN potential.

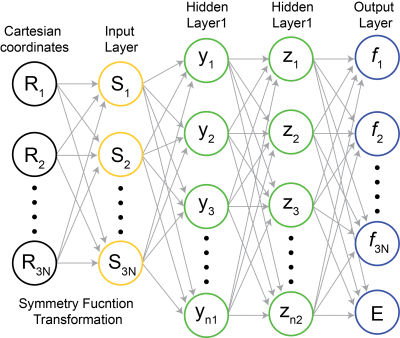
Here, we propose to develop an MD coupled self-evolving artificial neural-network (SE-ANN) potential. The proposed method begins with a fixed length of MD with FP-PES (collecting period), of which snapshots with corresponding energies and atomic forces will be recorded periodically. Afterward, a multi-target feed-forward NN,95 as illustrated in Figure 1, will be adapted to construct the ANN PES by training the dataset from collecting period. Symmetry functions developed by Behler will be used to transform Cartesian coordinates to input coordinates that are invariant to translation and rotation. By including the force vector (i.e., the gradient of PES) in the output layer, we expect a more accurate and faster learning of the PES than previous effort where only energy or other static property is set to be the target value.

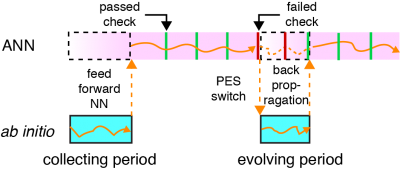
Another highlight of our method is the self-adaptivity. When the MD is running on ANN PES, the accuracy of the ANN model will be checked periodically. MD trajectory will switch back to FP-PES if the accuracy is under preset criteria. Meanwhile, self-evolution of ANN PES using back-propagation method will start simultaneously until the quality of prediction is recovered. The back-propagation method calculates the error contribution of each neuron using the new batch of FP dataset and updates the weight of each neuron. Figure 2 illustrates a typical run with the proposed MD coupled SE-ANN potential.

Our method can also be combined with other long-timescale simulation methods for extending the MD time scale, such as parallel replica dynamics, Hyperdynamics, and temperature acculturated dynamics.

The proposed research will lead to an innovative method to construct efficient and accurate ANN potentials for long-timescale simulations. Our short-term objective is to develop and implement the above scheme to an open source package, which interfaces with other machine learning and long-timescale simulation methods. In the long term, we aim to apply this novel method to investigate the dynamic coupling between morphology evolution and catalytic performance of NPs with a realistic size (d~2nm), which correlates with the study of supported NP morphology.